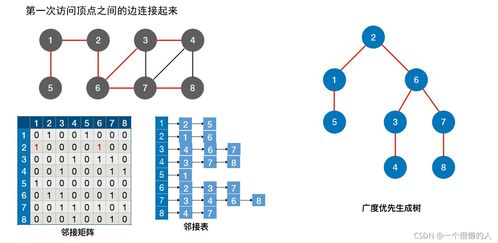
圖作為一種重要的非線性數據結構,廣泛應用于社交網絡、路徑規劃、網絡拓撲等領域。圖的遍歷是圖算法的基礎,其中深度優先搜索(DFS)和廣度優先搜索(BFS)是兩種最經典且核心的遍歷策略。高效的遍歷離不開底層數據結構的支持,即圖的存儲表示。本文將系統闡述DFS與BFS的原理、特點、應用場景,并深入探討為其提供支持的幾種關鍵存儲服務(鄰接矩陣、鄰接表等),分析不同存儲方式對遍歷性能的影響。
一、深度優先搜索(DFS)
深度優先搜索遵循“一條路走到黑,再回溯”的策略。其過程類似于樹的先序遍歷。
- 核心思想:從起始頂點出發,沿著某條路徑盡可能深地探索,直到該路徑上所有頂點均被訪問,然后回溯到上一個頂點,探索其未訪問的其他鄰接點,如此反復,直至圖中所有從起始點可達的頂點都被訪問。
- 實現方式:通常借助棧(遞歸調用棧或顯式棧)來實現回溯功能。遞歸實現代碼簡潔,體現了DFS天然的遞歸結構。
- 算法特點:
- 空間復雜度:在最壞情況下(如圖呈線性鏈狀),遞歸深度為O(|V|),其中|V|為頂點數。
- 時間復雜度:采用鄰接表存儲時為O(|V|+|E|)(|E|為邊數);采用鄰接矩陣則為O(|V|2),因為需要遍歷整個矩陣來尋找鄰接點。
- 生成樹/林:DFS遍歷過程中經過的邊會形成一棵深度優先樹(連通圖)或多棵深度優先樹組成的深度優先森林。
- 典型應用:拓撲排序、尋找連通分量、檢測圖中是否存在環、求解迷宮問題、尋找圖的關節點等。
二、廣度優先搜索(BFS)
廣度優先搜索遵循“層層推進”的策略,類似于樹的層序遍歷。
- 核心思想:從起始頂點出發,首先訪問其所有鄰接點,然后再按訪問順序,依次訪問這些鄰接點的未被訪問的鄰接點,以此類推,直到所有可達頂點都被訪問。
- 實現方式:必須借助隊列來管理待訪問的頂點,確保“先被發現的頂點先被訪問”。
- 算法特點:
- 空間復雜度:在最壞情況下需要存儲一整層的頂點,對于稠密圖可能達到O(|V|)。
- 時間復雜度:與DFS相同,鄰接表為O(|V|+|E|),鄰接矩陣為O(|V|2)。
- 最短路徑:在無權圖中,BFS從源點出發首次訪問到某個頂點的路徑,就是該頂點到源點的最短路徑。這是BFS一個極其重要的性質。
- 生成樹:BFS遍歷過程形成的是廣度優先樹。
- 典型應用:求解無權圖的最短路徑問題、社交網絡中查找“N度好友”、網絡廣播、GPS導航尋找最少換乘路線等。
三、圖的存儲支持服務
遍歷算法的效率與圖的具體存儲結構(即“存儲支持服務”)緊密相關。主要存儲方式有:
- 鄰接矩陣
- 表示方法:使用一個|V|×|V|的二維數組。對于無權圖,
matrix[i][j] = 1表示頂點i到j有邊,為0則表示無邊。對于帶權圖,可存儲權值。
- 遍歷支持分析:
- 優點:判斷任意兩個頂點間是否存在邊(即查詢操作)非常快,時間復雜度為O(1)。
- 缺點:空間開銷大,為O(|V|2),對于稀疏圖浪費嚴重。在遍歷時(尤其是BFS/DFS尋找某個頂點的所有鄰接點),需要掃描一整行,導致在稀疏圖上的遍歷效率較低。
- 鄰接表
- 表示方法:為每個頂點維護一個鏈表(或動態數組),鏈表中存儲與該頂點直接相鄰的所有頂點(對于帶權圖,可同時存儲權值)。
- 遍歷支持分析:
- 優點:空間復雜度為O(|V|+|E|),能高效利用稀疏圖的存儲空間。在遍歷時,能直接獲取一個頂點的所有鄰接點,無需掃描無效信息,這使得基于鄰接表的DFS/BFS時間復雜度優化至O(|V|+|E|)。
- 缺點:判斷任意兩個頂點間是否有邊,需要遍歷其中一個頂點的鏈表,效率為O(度(vertex)),不如鄰接矩陣。
- 其他存儲結構
- 十字鏈表:針對有向圖的優化存儲,結合了鄰接表和逆鄰接表,方便同時求取頂點的出邊和入邊。
- 鄰接多重表:針對無向圖的優化存儲,一條邊只用一個結點表示,避免了鄰接表中邊被存儲兩次的問題,適用于需要頻繁操作邊的場景。
四、與對比
| 特性 | 深度優先搜索 (DFS) | 廣度優先搜索 (BFS) |
| :--- | :--- | :--- |
| 數據結構 | 棧 (遞歸/顯式) | 隊列 |
| 遍歷順序 | 深度優先,縱向延伸 | 廣度優先,橫向擴展 |
| 解的性質 | 不保證最短路徑 | 保證無權圖最短路徑 |
| 空間消耗 | 與遞歸深度相關,通常較小 | 與每層寬度相關,可能較大 |
| 存儲服務影響 | 鄰接表效率遠高于鄰接矩陣 | 鄰接表效率遠高于鄰接矩陣 |
結論:DFS和BFS是圖遍歷的兩大支柱算法,選擇取決于問題本身(如求最短路徑必用BFS)。而鄰接表因其在稀疏圖中的空間高效性和遍歷時的直接性,成為實現這兩種算法最常用、最推薦的“存儲支持服務”。在實際系統(如社交網絡后端、推薦引擎)中,圖的存儲服務可能更為復雜,涉及分布式存儲、圖數據庫等,但其核心優化思想依然圍繞著如何高效地支持“查找某個頂點的所有鄰居”這一遍歷基本操作展開。理解基礎存儲結構與遍歷算法的關系,是設計和優化更高級圖處理系統的重要基石。